Math B - Geometry

---

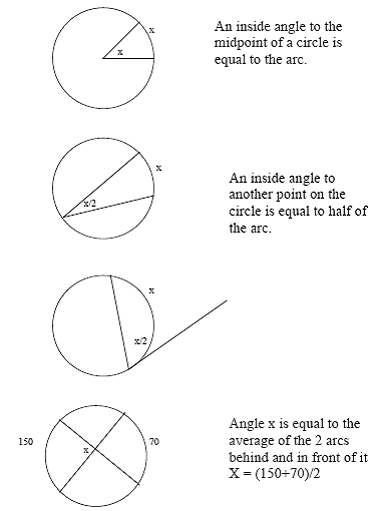
Circle Geometry

Quadrilaterals

The sum of the exterior angles of a regular polygon is 360.

 

 

Imaginary Numbers

 

�i� is just the square root of �1

Square root of �2 is 2i

This is because 1² =1, and (�1)²=1, so what is the square root of �1?...�i�

A quadratic equation will for sure have �i� in the answer if the radicand ((b²-4ac) is negative). 

 

Complex fractions

 

There are 3 rules:

Find the LCD.

Multiply each fraction by the LCD/1

Check for a 0 denominator.

   1 + 1

   3    5  .

       3

      10

 

The LCD is 2*3*5 so:

2*3*5              1

1            *        3

2*3*5              1

1            *        5

 

2*3*5              3

1            *        10

 

 Then you get

       10 + 6 .

       9

 

X      +    16         =      1

X+8     X²+64             X-8

 

X      +          16           =          1

X+8     (X+8)(X-8)               X-8

LCD: (X+8)(X-8)

 

Then you get:

X(X-8) + 16 = X+8...and solve as a quadratic.

You end up with the roots x=(8,1)

With 8 you get a 0 in one of the denominators, so it cancels out.

 

X-Y

Y-X  = -1

Radicals

 

A radical is a square root of number

   ___

\²/25     = 5

The 2 can be changed to find a different root of a number

   ___

\³/27     = 3

   ___

\⁴/256     = 4

If there is a radical in the denominator multiply the numerator and denominator by the conjugate of the denominator.

If you have:

1

(4- \²/25)

Multiply it by:

(4+ \²/25)

(4+ \²/25)

So you get:

(4+ \²/25)

(16-25) �..(4+5)/-9�.9/-9�..-1

 

Absolute values

First isolate the part in the absolute value

The make it into 2 problems...1 with the equasion taking away the absolute value signs, and 1 where you multiply what is in the signs by �1

Then check your answers

 

|X+1| = 2X+3

X+1 = 2X+3   |   -1(X+1) = 2X+3�-X-1 = 2X+3

X= -2              |   X= -4/3

|(-2)+1| = 1      |           |(-4/3)+1| = 1/3

2(-2)+3= -1      |           2(-4/3)+3 = 1/3

Doesn�t work  |           Works

 

 

Functions

A function tells you what to do with a number:

f(x)=3x

If I give you X, multiply it by 3

f(x) = 3X+15

g(x) = 2X

f o g(x) or  f(g(x))

= 3(2X)+15

g o f(x) or  g(f(x))

= 2(3X+15)

 

You change a function from being

f(x)=3x

Into: Y=3X

 If you want to find the f^-1(x) you just interchange the x and y, and solve for y:

f ^-1(x) of 3x

Y=3x

X=3y

A vector is just a horizontal line with the distance of a number.

A vector with length 5 looks like this:

A vector with a value multiplied by �i� is vertical.

When you add vectors you move the vectors, so that they are in head to tail orientation, and fin the resultant.

Add vectors 5+2i

Then find the resultant.

5²+2i²= R

 Exponential Equations

First find the common base

Then the 2 exponents are equal, so solve it.

 

81^x+2=27^5x+4

(3⁴)^x+2= (3³)^5x+4

3^4x+8= 3^15x+12

4x+8=15x+12

-11x = 4

X = -4/11

Logarithms

A^B=C

Log��_AC=B

Don�t need to know, but it helps:

Log��_AB =  Ln(B)          { ln() is a log with a natural base (different base) it is the button right

                 Ln(a)            under the log button on the claculator. }

X=log₂8

2^x=8

X= 3

 

If there is no specified base, it is 10.

Log(x*y) = log(x)+log(y)

Log(x/y) = log(x)-log(y)

Log(x²) = 2log(x)

Log(\/x) = 1/2Log(x)

Expand into logs:

P=q³z⁵

      \²/w

Log p = log(    q³z⁵            )

                                    \²/w

=log(q³z⁵)-log(\/w)

=(3log(q)+5log(z))-1/2log(w)

 

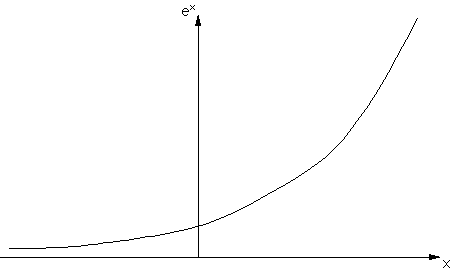
Exponential Curve

y is always positive

Crosses y axis at 1

Curve always rises

Asymptotic (gets close but never touches) x axis.

Y=5^x is an example of an exponential curve

Y=5^x

Hyperbole

Y=1/x

It is asymptotic to x and y axis.

Triginometry

Sin C = c/a = opposite/Hypotenuse

Sin B = b/a = opposite/Hypotenuse

Sin A = 1= opposite/Hypotenuse

Cos C = b/a= adjacent/hypotenuse

Cos B = c/a= adjacent/hypotenuse

Cos A = 0 = adjacent/hypotenuse

Tan B = b/c = opposite/adjacent

Tan C = c/b = opposite/adjacent

Tan A = error = opposite/adjacent

 

Csc C= a/c = 1/sinC

Csc B = a/b = 1/SinB

Csc A = 1 = 1/SinA

Sec C = a/b = 1/Cos C

Sec B = a/c = 1/CosB

Sec A = 0 = 1/Cos A

Cot C = b/c = 1/Tan C

Cot B = c/b = 1/Tan B

Cot A = error = 1/Tan A

 

SinA

CosA = TanA

 

Sin²A + Cos²A = 1

Sin (angle) = Cos (compliment)

Tan (angle) = Cot (complement)

Sec (angle) = Csc (complement)

 

Sin (angle) = y/distance

Cos (angle) = x/distance

Tan (angle) = y/x

Radian (angle) = arc/radius

To go from degree to radian, multiply by pi/180

To go from radian to degree multiply by 180/pi

 

Friendly angles

Sin (30) = 1/2   _

Sin (45) = 1/ (\/2 )

Sin (60) = (\/^�-3)/2

Sin (90) = 1

Sin (180) = 0

Sin (270) = -1

Sin (360) = 0

Cos (30) = (\/3)/2

Cos (45) = 1/(\/2)

Cos 60 = 1/2

Cos 90 = 0

Cos 180 = -1

Cos 270 = 0

Cos 360 = 1

Tan 30 = 1/(\/3)

Tan 45 = 1

Tan 60 = (\/3)

Tan 90 = error

Tan 180 = 0

Tan 270 = error

Tan 360 = 0

 

Cos (A-B) = (Cos A * Cos B) + (Sin A * Sin B)

Cos (A+B) = (Cos A * Cos B) - (Sin A * Sin B)

Cos 2X = Cos²X - Sin²X

Cos 2X = 1-2Sin²X

Cos 2X = 2Cos²X - 1

Sin (A-B) = (Sin A * Cos B) - (Cos A * Sin B)

Sin (A+B) = (Sin A * Cos B) + (Cos A * Sin B)

Sin 2X = 2 * Sin (X) * Cos (X)

Tan²X + 1 = Sec²X

Cot²X + 1 = Csc²X

c² = a² + b² - 2abCosC

   a          b            c  .

Sin A =  Sin B =  Sin C

 

Area of Triangle = (1/2)abSinC

 

 

 

 

 

 

Summation/sigma

 

 6

Σ k²

 K=2

 

You add up all the results you get from k² starting when k=2 (or whatever value specified on the bottom) and increment the value of k until it equals the number on top.

= 2² + 3² + 4² + 5² + 6²

 

 

 

Probability

 

General formula:

Prob(k successes in n trials) = (n nCr k) * (p)^k * (q)^n-k

 

n = number of trials
k = number of successes
n � k = number of failures
p = probability of success in one trial
q = 1 � p = probability of failure in one trial

Example:

You are taking a 10 question multiple choice test. If each question has four choices and you guess on each question, what is the probability of getting exactly 7 questions correct?

n = 10
k = 7
n � k = 3
p = 0.25 = probability of guessing the correct answer on a question
q = 0.75 = probability of guessing the wrong answer on a question

P(7 correct guesses out of 10 question)=(10 nCr 7) * (0.25)⁷ * (.75)³  ≈  0.0031

If the question had said �What is the probability of getting at least 7 correct.�  You would have needed to find the probability of getting 7 correct (above), then 8 correct, then 9 correct, then 10 correct. And then add up the probability of each.

If the question had said �What is the probability of getting 7 correct and getting 8 correct.�  You would have needed to find the probability of getting 7 correct (above), then 8 correct, and then multiply the probability of each.

 

Graphing

Slope:   Y_{2� ��}� Y₁

             X_{2� ��}� X₁

 

Distance:                                        .

                \/( X_{2� ��}� X₁)² + (Y_{2� ��}� Y₁)²

 

Midpoint:         average of Xs and Ys

 

Quadratic equations

 

General equation:   f(x)=ax² + bx + c

 

Quadratic formula to find the roots:

-b � √( b² � 4ac)

   X=                2a

When ( b² � 4ac), or the radicand, is zero the bases are equal

When the radicand is negative, the bases are imaginary and unequal

When the radicand gives a perfect square, you get unequal roots

When the radicand doesn�t give a prefect square, you get irrational and unequal roots

 

The sum of the roots will equal    �b/a

The product of the roots will equal      c/a

 

Sine, Cosine, and Tangent curves

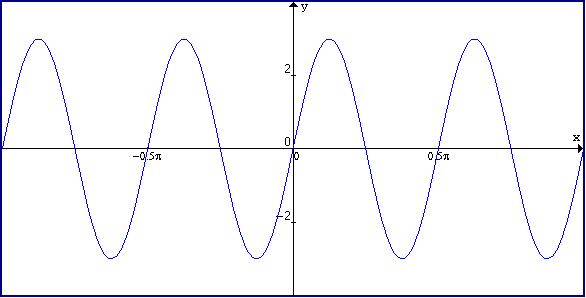
Sine curves generally look like this:

Saga of the Sine curve:

            The sine curve starts at the origin and rises gracefully reaching its zenith when the angle is ^Π/��₂ and then turns and descends gracefully crossing the x-axis when the angle is Π.            It continues its graceful decent reaching its nadir when the angle is ^3Π/��₂^. It turns again and ascends gracefully returning to the x-axis when the angle is 2Π.

Rules for sine curve:

When the function is f(x)=sin(3x), all the points where it intersects the x-axis must equal the angles listed above.

So we must do when 3x= ^Π/��₂, 3x= Π,3x= ^3Π/��₂, 3x= 2Π  and you get all the important points at whatever value x turns out to be

 

When the function is f(x)=3sin(x) the amplitude changes

The highest and lowest points(absolute extrema) are equal to 3 and -3

 

When the function is f(x)=sin(x)+5 it changes the height of the axis of symmetry.

In this function, the axis of symmetry would be 5.

 

So the equation for the graph above would equal:

F(x)= 3sin(4X) + 0

 

 

The cosine curve generally looks like this:

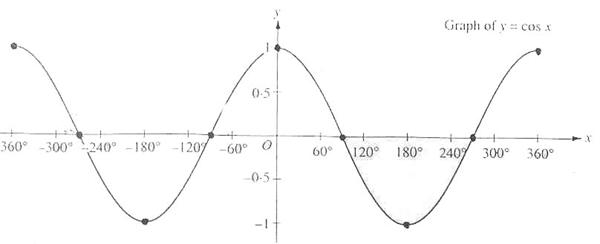
The cosine curve is similar to the sine curve, except that it starts at its zenith, and crosses the x-axis at ^Π/��_2, and ^3Π/��₂.

 

When the function is f(x)=cos(3x), all the points where it intersects the x-axis must equal the angles listed above.

So we must do when 3x= ^Π/��₂, 3x= Π,3x= ^3Π/��₂, 3x= 2Π  and you get all the important points at whatever value x turns out to be

 

When the function is f(x)=3cos(x) the amplitude changes

The highest and lowest points(absolute extrema) are equal to 3 and -3

 

When the function is f(x)=cos(x)+5 it changes the height of the axis of symmetry.

In this function, the axis of symmetry would be 5.

 

 

 

 

The tangent curve generally looks like this:

The tragic tale of the tangent:

            The tangent curve starts at the origin and rises quickly towards its asymptote, which occurs when the angle is ^Π/��₂. It rises more and more, getting closer and closer, when suddenly and mysteriously it appears on the other side of the asymptote and rises from its depths returning to the x-axis when the angle is Π.

 

Rules for tan curve:

 

When the function is f(x)=tan(3x), all the points where it intersects the x-axis must equal the angles listed above.

So we must do when 3x= ^Π/��₂, 3x= Π,3x= ^3Π/��₂, 3x= 2Π  and you get all the important points at whatever value x turns out to be

 

 

When the function is f(x)=3tan(x) the amplitude changes

The highest and lowest points(absolute extrema) are equal to 3 and -3

 

When the function is f(x)=tan(x)+5 it changes the height of the axis of symmetry.

In this function, the axis of symmetry would be 5.

 

 

Proofs

Properties:

 

Postulates:  (assumed to be true)

 

Theorems:  (can be proven true)

(Source http://regentsprep.org/Regents/mathb/1b/theorems.htm )

http://regentsprep.org/Regents/mathb/Proofs/AskedSoFarProofs.htm

 

 

 

 

 

Back to Top

---

Return to Junior Review Sheets

� Review Sheets Central

http://www.reviewsheetscentral.com